3日目(デバイスシミュレーション)
前回のSimple2Dの例題を走らせてみる。
まずは、Simple2Dのプロジェクトを開いてください。cd ~/work/Silicon/TCAD/Sentaurus/tutorials/Simple2D swb . &node 27だけ実行してあったと思います。 その構造に相当するIVシミュレーション(node 45)も実行して前回同様、Inspectorを使ってIV_n45_des.plt を開いてみてください。 anodeの OuterVoltage をx軸に、anodeのTotalCurrentをy軸に指定してプロットを描くとしたの図(左)のようになります。 最初の例題で見たグラフとずいぶん違う形になっていますが、これは130V付近で電場の集中による雪崩増幅が起こったことを示唆しています。 一般的に、p-n 接合に大きな逆方向電圧がかけられると,接合は降伏現象(Break down)を起こし,大電流が流れます。 Y軸をログスケールにするともう少しわかりやすいかもしれません。上の方真ん中付近にある logYというボタンを押してみてください。 下の図(右)のようになります。(対数グラフになっているので縦軸は絶対値になっているので注意! (0,0)は右下です。)
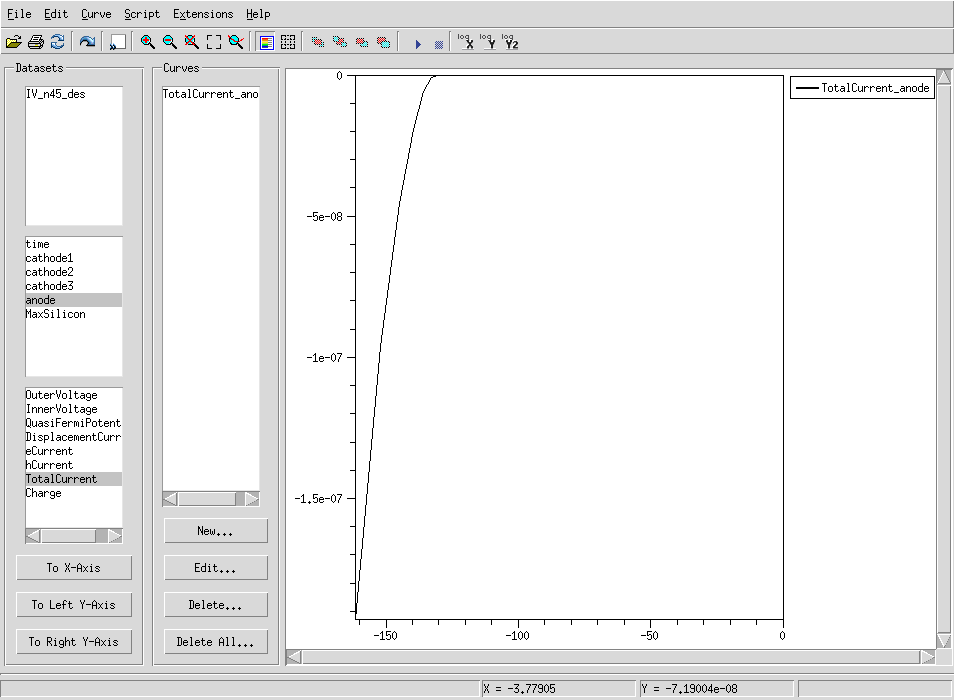
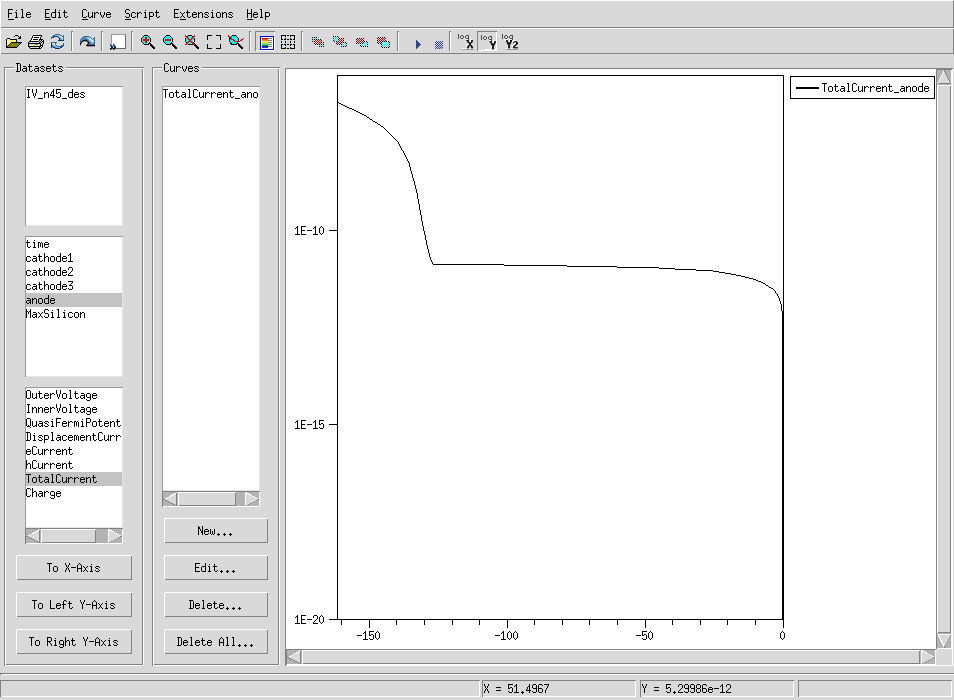 130V付近までは以前見た様な電流電圧特性を示しますが、その後急に増えていることがわかります。
この降伏(Break down)が起こる電圧をBreak down voltageと呼びます。
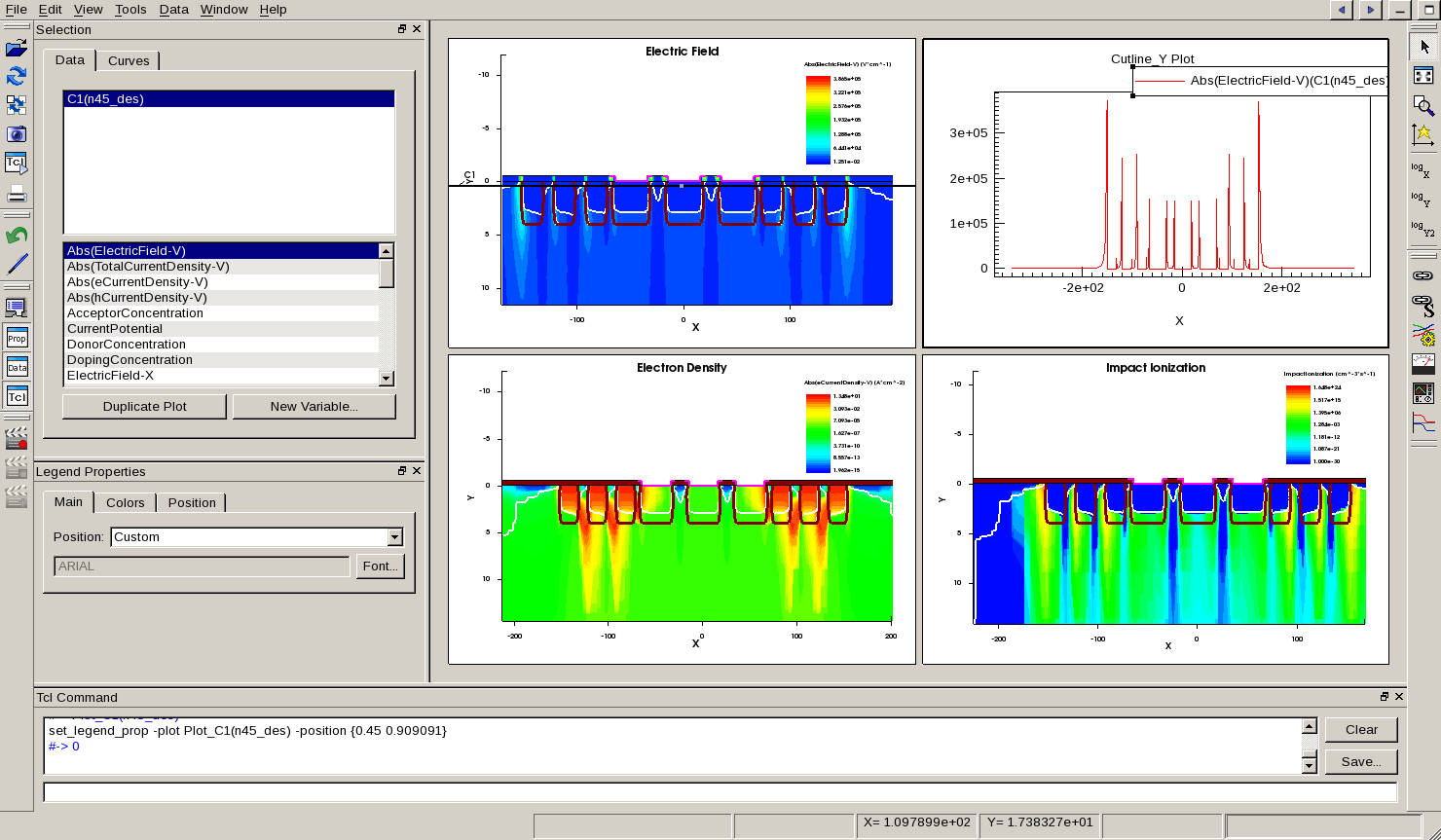
Breakを起こしたときの電場分布と電子の密度分布を見てみましょう。
node 45で右クリック、 svisual で n45_des.tdrを開く。
(scaling : X to Y ratioを10くらいにして表面領域を拡大してみてください。)
電場分布 (Electric Field)や、電子密度(Electron Density)、衝突イオン化(Impact Ionization)などを見てみるとガードリングの付近で非常に電場が集中していることがわかります。
一般的に電子の持つ運動エネルギーがシリコンのバンドギャップを超えたとき、雪崩増幅が起こります。この電圧はシリコンであれば約300kV/cm以上。(出典: SM.Sze. 『Semiconductor Device』3.7章「高電界効果」より)
電場分布をy軸に沿った軸でカットしてみると3e5V/cmを超えていることがわかります。
130V付近までは以前見た様な電流電圧特性を示しますが、その後急に増えていることがわかります。
この降伏(Break down)が起こる電圧をBreak down voltageと呼びます。
Breakを起こしたときの電場分布と電子の密度分布を見てみましょう。
node 45で右クリック、 svisual で n45_des.tdrを開く。
(scaling : X to Y ratioを10くらいにして表面領域を拡大してみてください。)
電場分布 (Electric Field)や、電子密度(Electron Density)、衝突イオン化(Impact Ionization)などを見てみるとガードリングの付近で非常に電場が集中していることがわかります。
一般的に電子の持つ運動エネルギーがシリコンのバンドギャップを超えたとき、雪崩増幅が起こります。この電圧はシリコンであれば約300kV/cm以上。(出典: SM.Sze. 『Semiconductor Device』3.7章「高電界効果」より)
電場分布をy軸に沿った軸でカットしてみると3e5V/cmを超えていることがわかります。
Simple2D のIVシミュレーションのコマンド
デバイスシミュレーションに関しては膨大なオプションが準備されています。マニュアルは全1574ページ!! もちろん今日だけで全部は説明できませんし、おそらく必要ないものがほとんどです。辞書的にマニュアルを使いながら理解してみてください。 IV_des.cmdという名前のファイルを見てみましょう。以下のコンポーネントからできています。File {...}
Electrode {...}
Physics {...}
CurrentPlot {...}
Solve {...}
Plot {...}
File section
まず初めに入力ファイルや出力ファイルを指定する。 入力ファイルは Gridとparameter。 Gridでは sdeで作った構造体を読み込みます。Work Benchでdevice simulationを行おうとしているnodeの左にあるSimple2Dというsdeを実行したノードの番号は @node|Simple2D@で取得できます。 parameterはシミュレーションに使う細かいパラメータを設定しています。通常はsdevice.parというファイルが使われます。 出力ファイルはCurrentとPlot が結果になります。 outputでlogを出力します。 Current (拡張子 plt) はすべてのシミュレーション(下のSolveで指定)の電極での電気的な結果の値が詰まったファイルを出力します。 @plotFile {
Grid = "n@node|Simple2D@_msh.tdr"
Current = "@plot@"
Plot = "@tdrdat@"
output = "@log@"
parameter = "@parameter@"
}
Electrode section
ここでは「電極」とその初期条件を指定します。IVなどのシミュレーションをする際にどこをGNDにどこを電位Vにするなどを指定する必要があります。 ただし、構造体をsdeで作った際に電極になる場所を作っておく必要があります。前回の sdegeo:define-contact-set を参照。 Simple2D_des.cmdのなかでストリップ電極(cathode1,2,3)+裏面(anode)の4つの電極を作って、それぞれを 0.0 Vに設定します。 eRecVelocity や hRecVelocityは再結合モビリティー(単位は cm/s)も指定できます。 そのほかに直列に抵抗を入れたり、電流や電荷の境界条件や初期条件を入れることができる。
Electrode {
!(
for {set i 1} {$i<=@NumStripes@} {incr i} {
puts "\{name = \"cathode${i}\" voltage = 0.0 eRecVelocity=1e7 hRecVelocity=1e7 \}"
}
)!
{name = "anode" voltage = 0.0 eRecVelocity=1e7 hRecVelocity=1e7 }
}
Physics section
物理モデルを指定する。この部分は来週、再来週にまとめて話します。
Physics {
##AreaFactor=1e8
##Fermi
}
Physics (material="Silicon") {
Mobility(
DopingDep (Unibo)
HighFieldsat (GradQuasiFermi)
)
Recombination(
SRH(DopingDep TempDep)
Auger
##hAvalanche(UniBo) eAvalanche(UniBo)
hAvalanche eAvalanche
)
EffectiveIntrinsicDensity (OldSlotboom)
Traps(
(
name="state1" acceptor conc=@<fluence*1.613>@
Level FromConductionBand EnergyMid =0.42
eXsection=2E-15 hXsection=2E-14
##eJfactor=1.0 hJfactor=1.0
)
(
name="state2" acceptor conc=@<fluence*100.0>@
Level FromConductionBand EnergyMid =0.46
eXsection=5E-15 hXsection=5E-14
##eJfactor=1.0 hJfactor=1.0
)
(
name="state3" donor conc=@<fluence*0.9>@
Level FromValenceBand EnergyMid =0.36
eXsection=2.5E-14 hXsection=2.5E-15
##eJfactor=1.0 hJfactor=1.0
)
)
}
CurrentPlot section
基本的に結果のアウトプットは二種類あります。- CurrentPlot : 拡張子が .plt のファイルで、各電極ごとに、Voltage, Current, Charge, Potencial等の情報が出力されます。svisual や inspectorで開くことができますが、ASCIIのテキストファイルなのでC++やPython、ROOTのプログラムで読み込むこともできます。
- Plot : 拡張子が .tdr のファイルで、構造体の各点での、電場や電流密度、衝突イオン化、粒子速度(モビリティー)などが出力されます。基本的にsvisualでしか開くことができません。
CurrentPlot {
eLifeTime(Maximum(material="Silicon"))
hLifeTime(Maximum(material="Silicon"))
eAvalanche(Maximum(material="Silicon"))
hAvalanche(Maximum(material="Silicon"))
}
Math section
デバイスシミュレータは(基本的には部分積分)方程式を各メッシュごとに、矛盾することなくイテレーション(反復)しながら解いていきます。 各 Iterationで適度に小さい誤差で数値が収束する必要があります。Math sectionでは数値解析の様々なオプションを設定します。 全部は説明しませんが、それぞれの項目が何を表しているかをSentaurus Device Usr Guide マニュアルのp.1432 Table 205を参照してください。
Math {
##CDensityMin=1e-100
Extrapolate
Derivatives
Avalderivatives
Digits=5
Notdamped=1000
Iterations=20
RelerrControl
ErrRef (electron)=1e6
ErrRef (hole)=1e6
RhsMin =1e-15
eMobilityAveraging=ElementEdge
hMobilityAveraging=ElementEdge
ParallelToInterfaceInBoundaryLayer (-ExternalBoundary)
##Method=Blocked
##SubMethod=ILS (set=1)
##Method=ILS (set=1)
Method=Pardiso
ILSrc = "
set(1) {
iterative( gmres(100), tolrel=1e-8, tolunprec=1e-4, tolabs=0, maxit=200 );
preconditioning( ilut(0.0001,-1), left );
ordering( symmetric=nd, nonsymmetric=mpsilst );
options( compact=yes, verbose=0, refineresidual=0 );
};
"
number_of_threads=4
}
Solve Section
デバイスシミュレーションでなんの解を求めてもらうかを指定する場所です。ここの部分が最も大事です。 初期条件、各シミュレーションステップでのコンディションを定義して解を見つけます。Solve {
Poisson
plugin { Poisson Electron Hole }
Coupled { Poisson Electron Hole }
ここまでが初期条件の定義です。電極を定義した際の初期設定を使って、実際に電位等の設定をします。
Poissonは、非線形のポアソン方程式のみを使って解を計算するということを指定しています。特殊な設定を必要とする場合はここに書きます。
Coupled{} では、Electron (電流の連続方程式) とPoisson (ポアソン方程式) の直接結合を考えるという意味です。静電容量で結合している場合はACCoupled{}を使います。
解は、前のステップからの推測値を初期条件にして計算します。
NewCurrent ="IV_"保存する CurrentPlot に接頭語"IV_"を付ける。
Quasistationary ( DoZero
MaxStep =1 MinStep =1e-8 InitialStep =1e-5
Increment=1.6 Decrement=4.0
Goal { Name="anode" Voltage=@Vop@}
BreakCriteria {Current (Contact = "anode" minval = -1e-7 )}
)
{ Coupled { Poisson Electron Hole } }
system("")
}
こののQuasistationaryで定義されている部分で、初期状態から終状態までのシミュレーションステップを定義します。
文字通り、各ステップで、準定常(Quasi-stationary)状態に収束するまで計算します。
文法は Quasistationary (ステップとゴールの条件){考慮する方程式} のようなイメージです。
ステップの定義は MaxStep, MinStep, InitialStep はそれぞれ最大のステップ、最小のステップ、最初のステップです。初期値からゴール値までをt=1とした時の割合で定義します。
つまり、Step 1e-5 でスキャンした場合は 10万回のステップを踏む必要があるのでとてつもない時間がかかります。
ステップサイズは自動的に調整されます。InitialStepでスキャンを始めて、収束しないようならステップサイズを小さくするという方針でステップを決めます。
ただし、収束した場合は、最大Increment分だけ大きなステップを使うことができるというアルゴリズムです。
基本的にシミュレーション時間が長すぎる場合は、このステップが細かすぎる、もしくは、各点の収束がうまくいっていないために、小さなステップでやり直すという作業を繰り返しているからです。
より安定した電場ができる構造体に直すか、必要ない場合はステップを粗くしてみるとよいです。
最初に見たInspectorのIVカーブのプロットに測定点のマーカーを付けてみると測定点がわかります。Curvesの中からプロットを選択、Editボタン、MarkerタブのShapeをcircleにする。OKをクリック。
もしくは、node 51のinspectを実行してみてください。
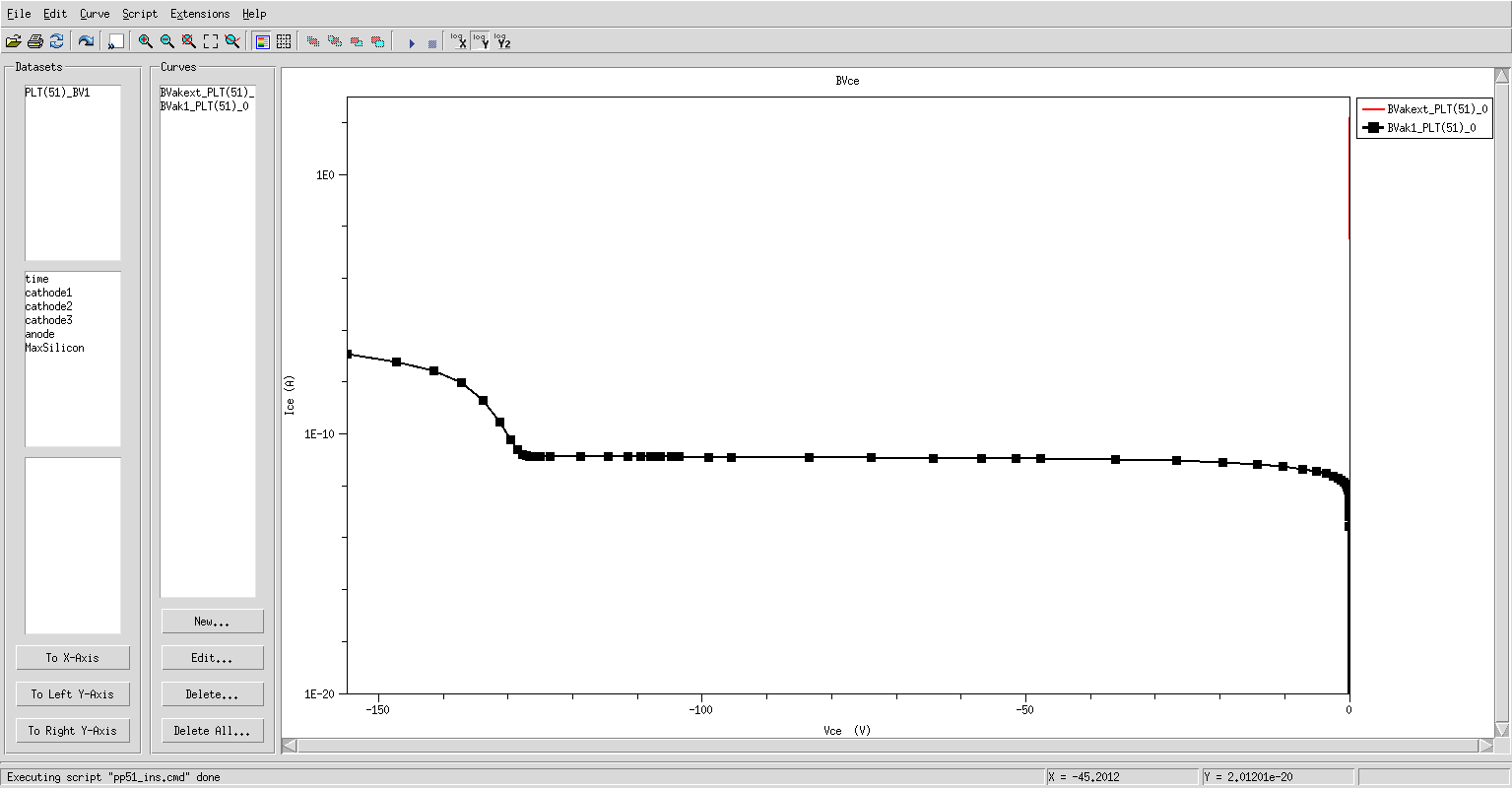 最初の部分は細かくだんだん粗くなっていき収束しない場合は再び細かくなっていることがわかります。
また、この例だと、Vop=-200Vと設定していますが、-150V付近で終わってしまっています。これは、BreakCriteria を使って電流が1e-7A(100nA)を超えたときに停止するようにしているからです。
node 51を実行して、inspectを閉じたときにWorkbenchの最初の行の一番右にBVakという変数ができて、154.9となっているのがわかります。これはブレークダウンを電流<-1e-7Aと定義したときの電圧の値を示しています。
ただし、上で説明したStepごとにしか計算を行っていないのでブレークダウンを起こした最初の電圧ステップを表示していることになります。
最初の部分は細かくだんだん粗くなっていき収束しない場合は再び細かくなっていることがわかります。
また、この例だと、Vop=-200Vと設定していますが、-150V付近で終わってしまっています。これは、BreakCriteria を使って電流が1e-7A(100nA)を超えたときに停止するようにしているからです。
node 51を実行して、inspectを閉じたときにWorkbenchの最初の行の一番右にBVakという変数ができて、154.9となっているのがわかります。これはブレークダウンを電流<-1e-7Aと定義したときの電圧の値を示しています。
ただし、上で説明したStepごとにしか計算を行っていないのでブレークダウンを起こした最初の電圧ステップを表示していることになります。
Plot Section
ここでは、Plotファイルに出力する変数のリストを定義します。Plot {
Current/Vector
eCurrent/Vector
hCurrent/Vector
eDensity
hDensity
ElectricField /Vector
Potential
CurrentPotential
DopingConcentration
eMobility
hMobility
DonorConcentration
AcceptorConcentration
AvalancheGeneration
eAvalanche hAvalanche
eLifeTime hLifeTime
}
様々なデバイスシミュレーション
静電容量のシミュレーション (C-Vシミュレーション)
まずは node 57を走らせてみましょう。C-Vシミュレーションです。 しばらく時間がかかるのでCV_des.cmdファイルの中身を見てみましょう。 IV_des.cmd と違う点は 新たに system sectionが導入されたことと、Solve sectionにACCoupled()が定義されたことです。System section
System sectionは一般的に回路を定義することに使います。SPICEという、回路シミュレータの構文が使われます。 しかし、ここでは基本的にanode とcathodeに a, c1,c2,c3という名前を付けて、 それぞれの電極にかける電圧を va,vc1,vc2,vc3と定義しているだけです。system {
DIODE D1 ("anode"=a
!(
for {set i 1} {$i<=@NumStripes@} {incr i} {
puts "\"cathode${i}\"=c${i}"
}
)!
) {}
Vsource_pset va (a gnd) {dc=0}
!(
for {set i 1} {$i<=@NumStripes@} {incr i} {
puts "Vsource_pset vc${i} (c${i} gnd) \{dc=0\}"
}
)!
set(gnd=0)
}
Solve section
次にSolve sectionですが、二つのQuasistationaryが定義されています。 Quasistationary ( DoZero
MaxStep=0.1 MinStep=5e-6 InitialStep=1e-2
Increment=1.6 Decrement=4.0
Goal { Parameter="va"."dc" Voltage=0.6 }
)
{ Coupled { Poisson Electron Hole } }
最初のQuasistationaryはIVの時と同様でCoupled{}のシミュレーションを行っています。
ただし、電圧の方向が順バイアスになっていることに注意。0.6Vまでの順バイアスをかけて電流電圧特性をシミュレーションしています。
NewCurrent="CV_"
Quasistationary ( DoZero
MaxStep=0.02 MinStep=5e-6 InitialStep=1e-4
Increment=1.6 Decrement=4.0
Goal { Parameter="va"."dc" Voltage=-100 }
)
{
ACCoupled (
StartFrequency=1.0 EndFrequency=1.0
NumberOfPoints=1 Decade
!(
set nodelist "a"
set sourcelist "va"
for {set i 1} {$i<=@NumStripes@} {incr i} {
set nodelist "$nodelist c${i}"
set sourcelist "$sourcelist vc${i}"
}
puts "Node($nodelist) Exclude($sourcelist)"
)!
) { Poisson Electron Hole }
}
新しくCV_という名前でプロットを定義した方のQuasistationaryは静電容量の電圧依存性をシミュレーションします。
二つ以上のQuasistationaryがある場合は一つ前の実行後の終状態を始状態として使います。つまり電圧は+0.6Vからのスタートです。
system sectionで定義したva変数を -100Vまで変化させます。ステップの定義の仕方は既に学習した通りです。
ACCoupled(){}が今回新しく出てきたものです。ACシミュレーションではLCRメータと同様にある周波数の電圧をかけることで測定します。
その周波数は StartFrequency と EndFrequency で定義されます。(単位は[Hz]) この例では1Hzの周波数、1点でシミュレーションを行っています。
AC解析はNode()でセットされた電極間での容量をシミュレーションします。この場合v*で定義したSourceのlistを除くすべての電極間でシミュレーションを行っています。
CV測定結果
走り終わったCV測定の結果を見てみてください。CV_n57_ac_des.pltをinspectorで開きます。 X軸を v(a) Y軸を c(a,c2) としてプロットさせるとC-V特性が見られます。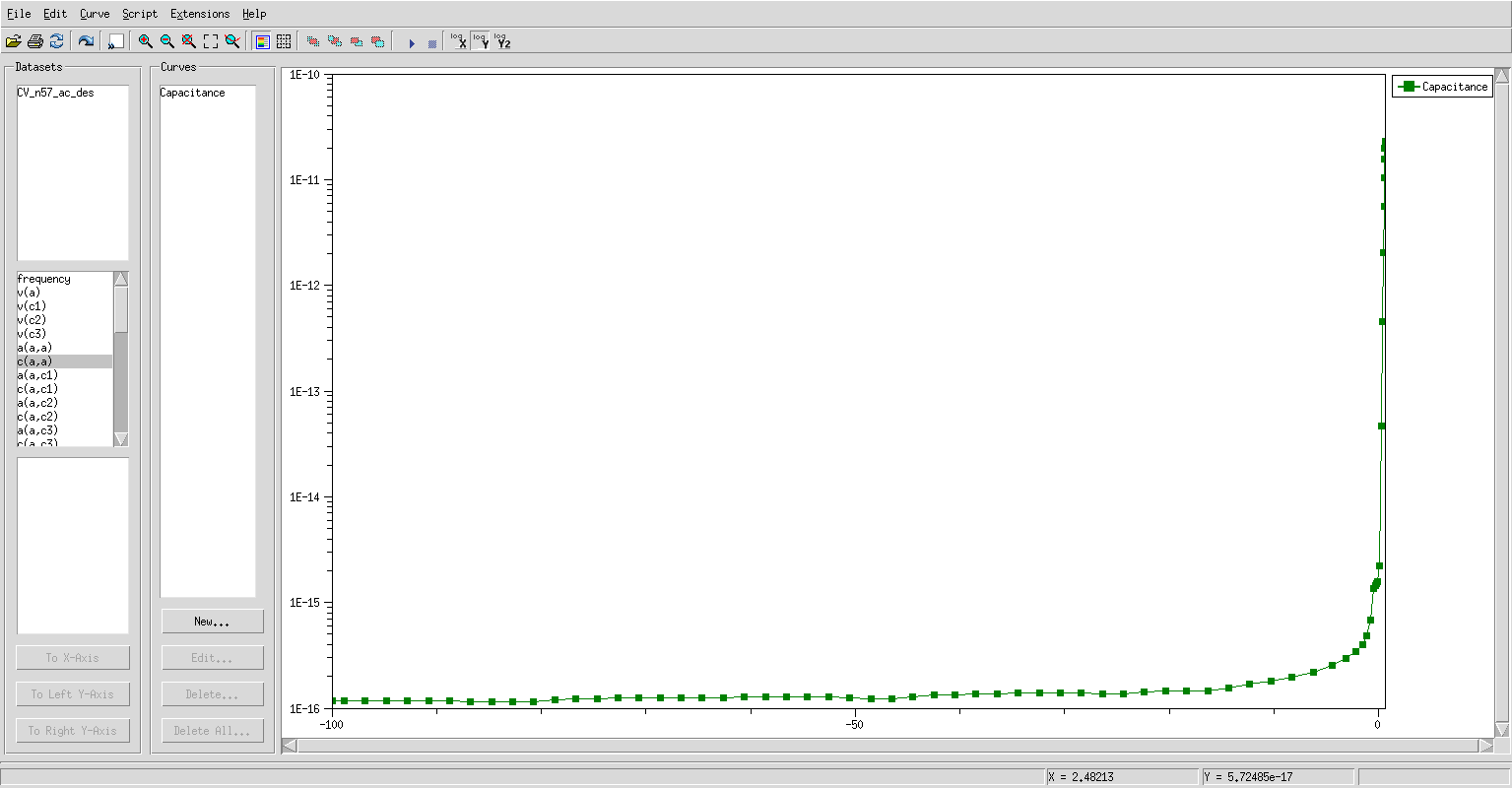 (inspectorでのプロットの扱い方をあまり知らないので... ) sdeviceで 1/c^2の電圧依存性を見てみましょう。
同じファイル(CV_n57_ac_des.plt)をsvisualで開きます。
NewValueとして、c(a,c1) + c(a,c2) + c(a,c3) をSumCapacitanceという変数にします。
(実際は、 <c(a,c1):CV_n57_ac_des>+<c(a,c2):CV_n57_ac_des>+<c(a,c3):CV_n57_ac_des> )
次に!NewValueとして 1/(SumCapacitance*SumCapacitance)を 1overCsqという変数名で作ります。
(実際は、1/(<SumCapacitance:CV_n57_ac_des>*<SumCapacitance:CV_n57_ac_des>))
1overCsqをv(a)の関数でプロットしてみてください。
(inspectorでのプロットの扱い方をあまり知らないので... ) sdeviceで 1/c^2の電圧依存性を見てみましょう。
同じファイル(CV_n57_ac_des.plt)をsvisualで開きます。
NewValueとして、c(a,c1) + c(a,c2) + c(a,c3) をSumCapacitanceという変数にします。
(実際は、 <c(a,c1):CV_n57_ac_des>+<c(a,c2):CV_n57_ac_des>+<c(a,c3):CV_n57_ac_des> )
次に!NewValueとして 1/(SumCapacitance*SumCapacitance)を 1overCsqという変数名で作ります。
(実際は、1/(<SumCapacitance:CV_n57_ac_des>*<SumCapacitance:CV_n57_ac_des>))
1overCsqをv(a)の関数でプロットしてみてください。
 電圧に比例するはずですが、シミュレーションではちょっといびつな形をしています。
おそらく今回のシミュレーションのデバイスの大きさが小さいこと、cathode電極に対してanodeが広いことで、上に凸の形になったのかもしれません。
電圧に比例するはずですが、シミュレーションではちょっといびつな形をしています。
おそらく今回のシミュレーションのデバイスの大きさが小さいこと、cathode電極に対してanodeが広いことで、上に凸の形になったのかもしれません。
荷電粒子通過のシミュレーション (MIPシミュレーション)
まずは node 81を走らせてみましょう。MIP粒子通過のシミュレーションです。 しばらく時間がかかるのでMIP_des.cmdファイルの中身を見てみましょう。 IV_des.cmdと異なる点は Physicsモデルに HeavyIonが加わっていることと、Quasistationaryではなく、Transientが使われていることです。HeavyIonのPhysicsモデル
Physics sectionに以下が追加されています。 これは単に時刻5e9s後に長さL幅whiの形に、1umあたり0.01pCの一様な電荷を置いているだけです。 HeavyIon("ion1") (
Direction=(@dirX@,@dirY@)
Location=(@posX@,@posY@)
Time=@<0.0 + 5e-9>@
Length = @L@
LET_f = 0.01
Wt_hi = @whi@
Gaussian
PicoCoulomb
)
Solve section
最初の部分は電圧を-100Vまでかけています。 (いきなり-100Vの初期値を与えるのではなくIVの時と同様小さいステップで上げています。) Quasistationary ( DoZero
MaxStep=0.1 MinStep=1e-8 InitialStep=1e-3
Increment=2.0 Decrement=4.0
Goal { Name="anode" Voltage=@<-HV>@ }
##BreakCriteria {Current (Contact = "anode" minval = -1e-9 )}
)
{ Coupled { Poisson Electron Hole } }
#endif
#if 1==0
load(FilePrefix="n@node|IRRADIATION@")
#endif
以下が、電圧-100Vに固定して電荷を置いた時に時間とともに電場分布や電荷がどのように動くかをシミュレーションする部分です。
NewCurrent="MIP_"
Transient (
initialtime=0 finaltime=@<0.0+100.0e-9>@
##initialtime=0 finaltime=100.0e-9
###MaxStep=1e-8
MaxStep=10
MinStep=1e-18 InitialStep=1e-10
Increment=1.6 Decrement=4.0
TurningPoints(
( condition ( Time( range=( 0 @<0.0 + 5e-9 - 5e-11>@ ))) value=1e-10 )
( condition ( Time( @<0.0 + 5e-9 - 5e-11>@) ) value=2e-12 )
( condition ( Time( range=( @<0.0 + 5e-9 - 5e-11>@ @<0.0 + 5e-9 + 5e-11>@ ))) value=2e-12 )
)
)
{
Coupled { Poisson Electron Hole }
Plot(FilePrefix="n@node@_" time=(@<0.0 + 5e-9>@;@<0.0 + 5.02e-9>@;@<0.0 + 5.1e-9>@;@<0.0 + 5.2e-9>@;@<0.0 + 5.5e-9>@) nooverwrite )
}
Transientというコマンドを使います。これは時間発展のシミュレーションに用います。ここではstepで変えているのはtimeです。それ以外のコンディションは一つ前のコマンドの終状態で決まります。つまり、電圧が-100Vかかった状態でのシミュレーションとなります。ステップの決め方はQuasistationary の時と同じです。追加で、time rangeごとにステップを指定することができます。Turingpointというコマンドを使います。
あるtime rangeのstepを指定しているのがTurningPoints コマンドの次の3行です。5e-9[s]後に電荷が置かれるので、その5e-11[s]前までは1e-10[s]ステップ、その後は2e-12ステップでシミュレーションを行います。
計算自体はIVの時と同じで、Coupled{}で行います。各時刻でのPlotを保存するために Plot()を使います。この場合 5e-9 [s]後から、0ps,20ps,100ps,200ps,500ps 後のPlotを保存します。
Mipシミュレーションの結果
まずは node 81のジョブが終わっていたら結果を見てみましょう。MIP_n81_des.pltにCurrentPlotの結果が、n81__XXXX_des.tdrに時間ごとのPlotが保存されています。 n81__0000_des.tdr :0ps後 n81__0001_des.tdr :20ps後 n81__0002_des.tdr :100ps後 n81__0003_des.tdr :200ps後 n81__0004_des.tdr :500ps後 MIP_n81_des.pltから timeを横軸TotalCurrentやChargeを縦軸にしたプロットを作って、n81__XXXX_des.tdrから eDensityをプロットしてみると以下のようになります。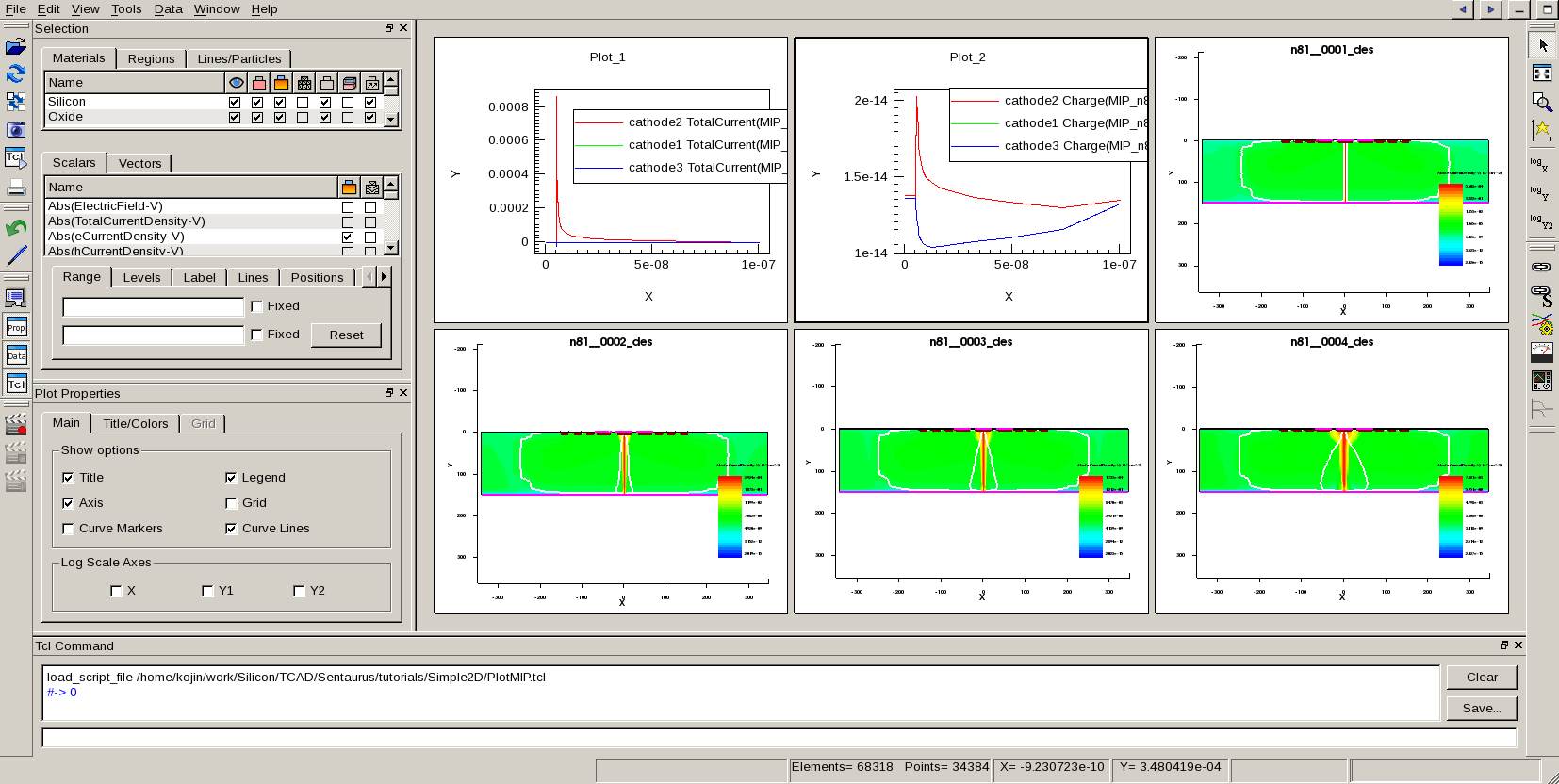 今日はここまでです。
演習課題 Tutorial4thTCADDay3Question に進んでください。
--
今日はここまでです。
演習課題 Tutorial4thTCADDay3Question に進んでください。
-- | I | Attachment | History | Action | Size | Date | Who | Comment |
|---|---|---|---|---|---|---|---|
| |
1overC2marker.png | r1 | manage | 67.1 K | 2020-05-26 - 15:35 | AtlasjSilicon | |
| |
CVmarker.png | r1 | manage | 10.6 K | 2020-05-26 - 15:19 | AtlasjSilicon | |
| |
IVmarker.png | r1 | manage | 11.3 K | 2020-05-26 - 14:25 | AtlasjSilicon | |
| |
field.png | r1 | manage | 102.4 K | 2020-05-21 - 08:53 | AtlasjSilicon | |
| |
iv_break.png | r1 | manage | 8.7 K | 2020-05-21 - 03:11 | AtlasjSilicon | |
| |
iv_break_ly.png | r1 | manage | 8.5 K | 2020-05-21 - 03:15 | AtlasjSilicon | |
| |
mipplot.png | r1 | manage | 106.6 K | 2020-05-27 - 08:31 | AtlasjSilicon |
Topic revision: r12 - 2020-05-28 - AtlasjSilicon
Ideas, requests, problems regarding TWiki? Send feedback





